SHOP > Info-Tafeln Lernen > Differentialrechnung
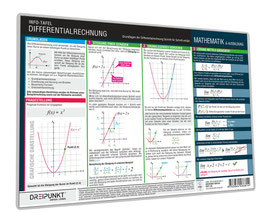
Differentialrechnung
Grundlagen der Differentialrechnung Schritt für Schritt erklärt.
Mit der Differentialrechnung können wir die Steigung einer Kurve an einem beliebigen Punkt berechnen.
Die korrekte Vorgehensweise ist hierbei für ein richtiges Ergebnis unerlässlich und kann besonders Einsteigern Schwierigkeiten bereiten. Auf dieser Info-Tafel findest du alles, was du für eine
erfolgreiche Differentialrechnung benötigst, auf einen Blick!
Du möchtest dein Wissen festigen?
Du benötigst einen zuverlässigen Helfer bei der Nachhilfe?
Du hast ein allgemeines Interesse an der Mathematik?
Diese Info-Tafel erleichtert dir den Einstieg (oder Wiedereinstieg) in die Differentialrechnung - übersichtlich, klar und mit Beispielen versehen.
Aus dem Inhalt:
- Grundlagen
- Fragestellung
- Steigung einer Geraden
- Grundlegendes Vorgehen
- Lösung mittels Grenzwert
- Funktion und Ableitung
- Anwendung der Ableitung
- Grenzwert
Optimal einzusetzen in Schule, Ausbildung, Studium und Beruf, bei der Nachhilfe (auch zum Selbststudium) sowie zum Auffrischen nach längerer 'Mathe-Abstinenz'.
7,95 €
inkl. MwSt, zzgl. Versandkosten
Versandkostenfrei in folgende Länder: Mehr anzeigen Weniger anzeigen
- verfügbar
- 1 - 2 Tage Lieferzeit
Hinweise zur Info-Tafel:
Größe: Papier DIN A4 (297 x 210 mm Querformat), Laminierung 303 x 216 mm mit technisch bedingten geringen Abweichungen (< 1mm)
Druck & Papier: Zweiseitiger hochwertiger 4-farb CMYK-Offsetdruck auf 90g SOPOR-SET-Papier, hochweiß
Laminierung: Heißlaminierung 500 mic ( 2 x 250 mic), hochglänzend, PET Polyester, glasklar, wasserfest#
Sprache: deutsch
Pflegehinweis: Vermeide 'scharfe' Putzmittel. Die
Laminierung kann dadurch ihren Glanz und im schlimmsten Fall ihre Durchsichtigkeit verlieren. Verwende ausschließlich handwarmes oder kaltes Wasser und gegebenenfalls ein handelsübliches
Abwaschmittel.
Hier geht es mathematisch weiter ...
DREIPUNKT®
Schulze Media GmbH
Meeschestraße 2
D-31246 Ilsede
Fon 0 51 72 . 27 12
Angaben zur Produktsicherheit
Hersteller:
Schulze Media GmbH
Meeschestraße 2
D-31246 Ilsede
info@dreipunkt-verlag.de
Copyright (c) DREIPUNKT® - Schulze Media GmbH